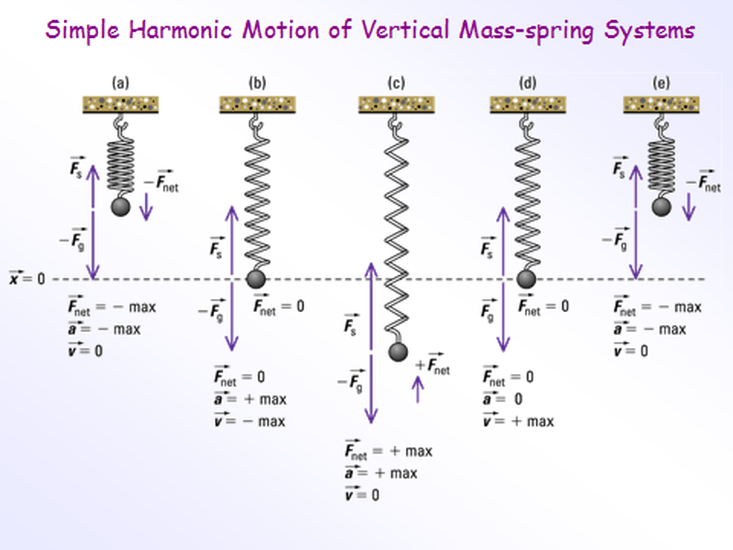
Four mass spring systems oscillate in simple harmonic motion, an intriguing phenomenon that unravels the complexities of oscillatory motion. This exploration delves into the fundamental concepts of frequency, amplitude, and phase, unveiling the intricate relationship between displacement, velocity, and acceleration within these systems.
Prepare to embark on a journey that illuminates the captivating dynamics of mass-spring systems and their diverse applications.
As we delve deeper into the topic, we will uncover the fundamental components of mass-spring systems, unraveling the concept of restoring force and exploring the factors that govern their natural frequency. The intricate interplay of multiple mass-spring systems will be examined, shedding light on the various types of coupling and their profound effects on the system’s behavior.
Oscillatory Motion
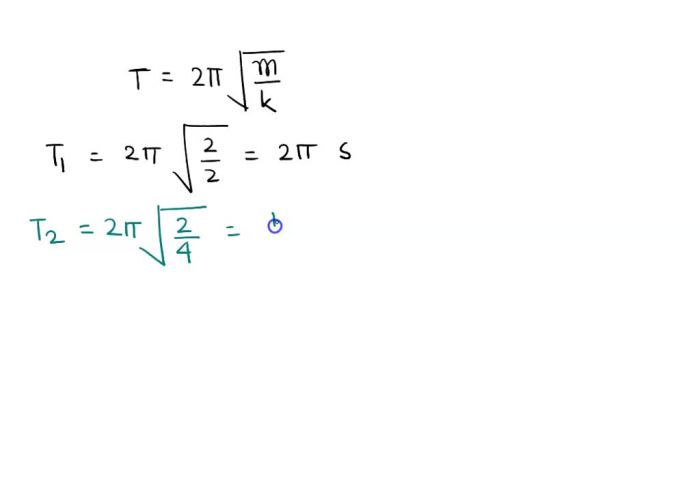
Oscillatory motion refers to the periodic motion of an object around an equilibrium position. Simple harmonic motion (SHM) is a specific type of oscillatory motion where the object moves back and forth along a straight line with constant amplitude and frequency.
SHM is characterized by three key parameters:
- Frequency: The number of oscillations per unit time, measured in Hertz (Hz).
- Amplitude: The maximum displacement of the object from its equilibrium position.
- Phase: The angle that represents the starting point of the oscillation.
The relationship between displacement, velocity, and acceleration in SHM is sinusoidal. The displacement is proportional to the sine of the phase angle, the velocity is proportional to the cosine of the phase angle, and the acceleration is proportional to the negative sine of the phase angle.
Mass-Spring Systems
A mass-spring system consists of a mass attached to a spring. The spring exerts a restoring force on the mass, which causes it to oscillate around its equilibrium position.
The restoring force is given by F = -kx, where k is the spring constant and x is the displacement of the mass from its equilibrium position.
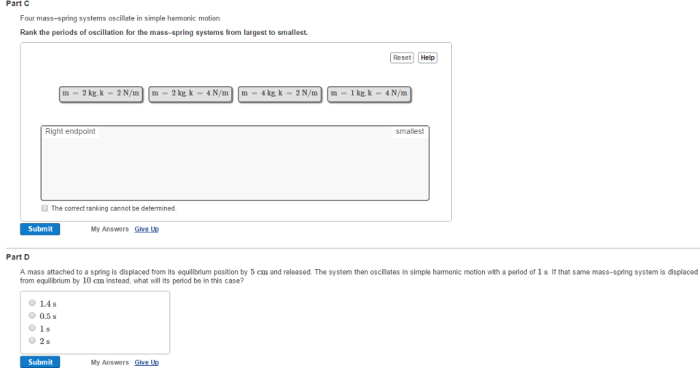
The natural frequency of a mass-spring system is given by f = 1/(2π)√(k/m), where m is the mass attached to the spring.
Multiple Mass-Spring Systems, Four mass spring systems oscillate in simple harmonic motion
Multiple mass-spring systems can be coupled together, meaning that the motion of one mass affects the motion of the others.
There are two main types of coupling: direct coupling and indirect coupling.
- Direct coupling: The masses are connected directly to each other, either through a spring or a rigid connection.
- Indirect coupling: The masses are connected through a common spring or through a fluid.
The coupling between masses affects the system’s behavior. For example, the natural frequencies of the system can change, and the system can exhibit more complex oscillations.
Applications of Mass-Spring Systems
Mass-spring systems have a wide range of applications in engineering, physics, and other fields.
- Vibration isolation: Mass-spring systems can be used to isolate vibrations from sensitive equipment.
- Energy storage: Mass-spring systems can be used to store energy in the form of potential energy.
- Clocks and watches: Mass-spring systems are used in clocks and watches to regulate the timekeeping.
Mass-spring systems are also used in a variety of other applications, such as suspension systems in vehicles, shock absorbers, and musical instruments.
Questions Often Asked: Four Mass Spring Systems Oscillate In Simple Harmonic Motion
What is simple harmonic motion?
Simple harmonic motion is a periodic motion where the restoring force is directly proportional to the displacement from the equilibrium position and acts in the opposite direction.
What are the factors that affect the natural frequency of a mass-spring system?
The natural frequency of a mass-spring system is determined by the mass of the object and the stiffness of the spring.
How can multiple mass-spring systems be coupled?
Multiple mass-spring systems can be coupled through mechanical connections, such as springs or dampers, or through electromagnetic forces.